kao.math.qp.QP Class Reference

Provides methods for solving Quadratic Programs (QP). More...

List of all members.

Classes
class	Out
	A definition of the outputs from the QP routines. More...
Static Public Member Functions
static Out	qp (Matrix G, Vector d0, Matrix Aeq, Vector beq, Matrix Aineq, Vector bineq, int maxIter, Vector A0)

---

Detailed Description

Provides methods for solving Quadratic Programs (QP).

Author:

David Kao

---

Member Function Documentation

static Out kao.math.qp.QP.qp	(	Matrix	G,
		Vector	d0,
		Matrix	Aeq,
		Vector	beq,
		Matrix	Aineq,
		Vector	bineq,
		int	maxIter,
		Vector	A0
	)			[static]

This routine calls a dual method for solving strictly convex quadratic programs of the form:

min f(x) = 0.5x'Gx + d0'x

s.t Aineq x - bineq >= 0 Aeq x - beq = 0

such that

where:

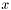• is a column vector of length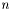
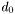• is a column vector of length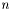
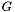• is a 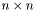positive definite matrix
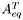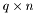• is a matrix where each row defines an equality constraint
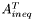• is a 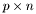matrix where each row defines an inequality constraint
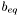• is a column vector of length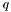
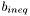• is a column vector of length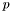

This method is based on Goldfarb [1]. In addition a set of active constraints 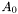calculated from an initial guess can be passed into the algorithm.

[1] D. Goldfarb and A. Idnani A numerically stable dual method for solving strictly convex quadratic problems, Mathematical Programming 27, 1983, 1-33.

Parameters:

[in]	G	Hessian of QP
[in]	d0	Vector of QP
[in]	Aeq	Equality constraint matrix
[in]	beq	Equality constraint vector
[in]	Aineq	Inequality constraint matrix
[in]	bineq	Inequality constraint vector
[in]	maxIter	Max iterations
[in]	A0	Initial active set guess

Returns:

Out.x Solution of QP

Out.f Cost at solution

Out.iter Number of iterations

Out.u Lagrange Multipliers

Out.A List of active constraints

Out.C History of active constraints

Author:

David Kao